Bài toán (Đề thi thử VMO 2015 Viện Toán Học)
Cho tam giác  nhọn nội tiếp đường tròn
nhọn nội tiếp đường tròn 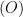 . Gọi
. Gọi  là trung điểm của
là trung điểm của 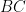 và
và  là trực tâm tam giác
là trực tâm tam giác  . Cho
. Cho  cắt
cắt  tương ứng tại
tương ứng tại  . Tia
. Tia  cắt
cắt 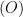 tại
tại  . Trên đường thẳng
. Trên đường thẳng  lấy điểm
lấy điểm 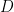 sao cho
sao cho  song song
song song 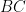 .
.
a) Chứng minh  tiếp xúc với
tiếp xúc với  .
.
b) Gọi 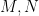 là giao theo thứ tự của
là giao theo thứ tự của  với
với  thoả
thoả  khác phía
khác phía  đối với
đối với 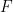 và
và  khác phía
khác phía 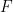 đối với
đối với  . Gọi
. Gọi  là giao của
là giao của  với
với 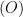 . Chứng minh
. Chứng minh  đồng quy.
đồng quy.
Lời giải :
a) Theo định lí Brocard thì  vuông góc
vuông góc  , điều này cho ta
, điều này cho ta  thuộc
thuộc  .
.
Gọi 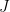 là giao
là giao 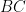 với
với  . Vì
. Vì  hay
hay 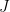 có cùng phương tích với
có cùng phương tích với  và
và 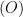 . Suy ra
. Suy ra 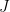 thuộc trục đẳng phương của chúng, tức
thuộc trục đẳng phương của chúng, tức 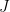 thuộc
thuộc  .
.
Ta thấy :
Điều này chứng tỏ là  là tiếp tuyến của
là tiếp tuyến của  .
.
Mặt khác,  song song
song song 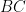 và
và  là trung điểm của
là trung điểm của 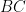 nên suy ra
nên suy ra  .
.
Hay là  . Suy ra tứ giác
. Suy ra tứ giác  điều hoà, lại có
điều hoà, lại có  cắt tiếp tuyến tại
cắt tiếp tuyến tại  của
của  tại
tại 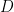 nên
nên  là tiếp tuyến của
là tiếp tuyến của  .
.
b) Ta có  và
và  vuông góc
vuông góc  nên theo định lí chùm điều hoà ta có
nên theo định lí chùm điều hoà ta có  là phân giác góc
là phân giác góc  hay
hay  .
.
Hơn nữa  và
và  vì
vì  là trung điểm cạnh huyền
là trung điểm cạnh huyền 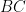 của tam giác vuông
của tam giác vuông  .
.
Kéo theo  . Điều này cho ta
. Điều này cho ta  nội tiếp hay
nội tiếp hay  .
.
Từ đó :
Suy ra  là tiếp tuyến tại
là tiếp tuyến tại 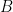 của
của 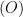 . Tương tự
. Tương tự  là tiếp tuyến tại
là tiếp tuyến tại  của
của 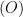 .
.
Hơn nữa có  nên tứ giác
nên tứ giác  điều hoà. Suy ra
điều hoà. Suy ra  và hai tiếp tuyến tại
và hai tiếp tuyến tại  của
của 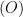 đồng quy. Tức là
đồng quy. Tức là  đồng quy.
đồng quy.
Hoàn tất bài toán.

Nhận xét
Đăng nhận xét