- Nhận đường liên kết
- X
- Ứng dụng khác
Phương pháp Vieta Jumping (Bước nhảy Viete)
Arithmetic Sequence
Bài toán : Xét phương trình 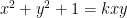 .
.
a) Tìm tất cả các số 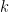 nguyên dương sao cho phương trình trên có nghiệm nguyên dương
nguyên dương sao cho phương trình trên có nghiệm nguyên dương 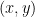 .
.
b) Với các giá trị 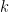 tìm được, hãy tìm tất cả các nghiệm nguyên dương của phương trình.
tìm được, hãy tìm tất cả các nghiệm nguyên dương của phương trình.
Lời giải :
a) Cố định 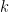 và xét tập :
và xét tập :
Trong  chọn ra cặp
chọn ra cặp  thỏa mãn
thỏa mãn  nhỏ nhất, giả sử
nhỏ nhất, giả sử 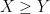 .
.
Xét phương trình :
Dễ thấy phương trình này có nghiệm 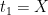 , gọi nghiệm còn lại là
, gọi nghiệm còn lại là 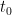 . Theo định lí Viete :
. Theo định lí Viete :
Từ đây dễ thấy 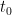 cũng nguyên dương, vì tính nhỏ nhất của
cũng nguyên dương, vì tính nhỏ nhất của  nên
nên  .
.
Suy ra :
Vì  nguyên dương nên
nguyên dương nên 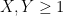 . Như vậy :
. Như vậy :
Và dấu bằng chỉ xảy ra khi 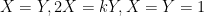 . Mâu thuẫn. Như vậy
. Mâu thuẫn. Như vậy  . Hơn nữa theo AM-GM ta dễ thấy
. Hơn nữa theo AM-GM ta dễ thấy  .
.
Ta được 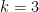 . Thử lại với
. Thử lại với 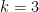 thì
thì  là một nghiệm của phương trình.
là một nghiệm của phương trình.
b) Ta tìm tất cả các nghiệm của phương trình :
Xét dãy số  xác định như sau :
xác định như sau :
Ta chứng minh nếu 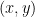 là cặp số nguyên dương bất kỳ thỏa
là cặp số nguyên dương bất kỳ thỏa 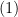 khi và chỉ khi
khi và chỉ khi  để
để  .
.
Thực vậy, dễ kiểm tra được 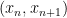 thỏa
thỏa 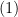 với mọi
với mọi  . Gọi
. Gọi  là một cặp số nguyên dương bất kỳ thỏa
là một cặp số nguyên dương bất kỳ thỏa 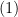 . Nếu
. Nếu  thì
thì  , tức tồn tại
, tức tồn tại  để
để  . Do đó ta chỉ cần xét
. Do đó ta chỉ cần xét  , giả sử luôn
, giả sử luôn  .
.
Khi đó ta chọn  . Dễ thấy
. Dễ thấy 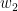 nguyên dương và cặp
nguyên dương và cặp  lúc này cũng thỏa
lúc này cũng thỏa 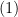 .
.
Để ý ta có :
Suy ra  .
.
Hoàn toàn tương tự ta chọn được cặp 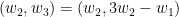 cũng thỏa
cũng thỏa  nguyên dương và
nguyên dương và  .
.
Cứ tiếp tục quá trình này, ta được :
Nhưng  bị chặn dưới bởi
bị chặn dưới bởi 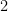 nên phải tồn tại
nên phải tồn tại 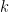 sao cho :
sao cho :
Từ đó :
…
Như vậy với cặp  bất kỳ thì tồn tại
bất kỳ thì tồn tại  để
để 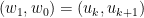 .
.
Từ đó tất cả các nghiệm của phương trình là  với dãy
với dãy  xác định như trên.
xác định như trên.
Lưu ý : Kỹ thuật xét dãy như trên :
Xét dãy truy hồi tuyến tính cấp hai :
Để ý thì thấy :
Như vậy :
Do đó nếu gặp phương trình có dạng :
Thì ta sẽ xét dãy  .
.
- Nhận đường liên kết
- X
- Ứng dụng khác
Nhận xét
Đăng nhận xét